ChimeraX Recipes

Show a rotational diffusion tensor ellipsoid

Arun Gupta asked on the ChimeraX mailing list about how to display a rotational diffusion tensor computed by ROTDIF software as a mesh ellipsoid. ROTDIF produces a PyMol Python script (for example ELM_ellipsoid.py) to show the ellipsoid. Here we make a similar script for ChimeraX.

At first it seemed the ChimeraX command shape ellipsoid would do the job. But the mesh pattern for the ellipsoid is not latitude and longitude lines, instead it uses a spiral triangulation for best ellipsoid surface smoothness. So the code below instead makes the latitude and longitude lines.

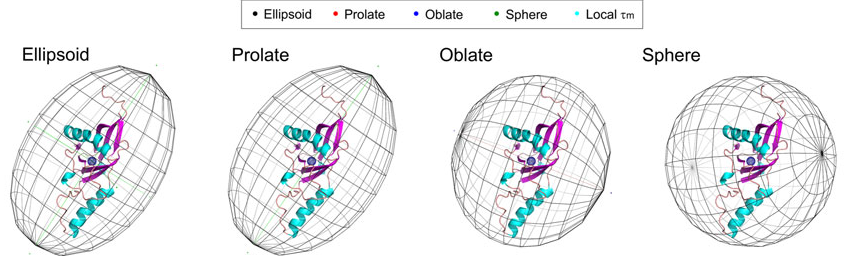
Here is an image Arun provided illustrating what is desired

And here is an example of the ellipsoid produced by the ChimeraX script

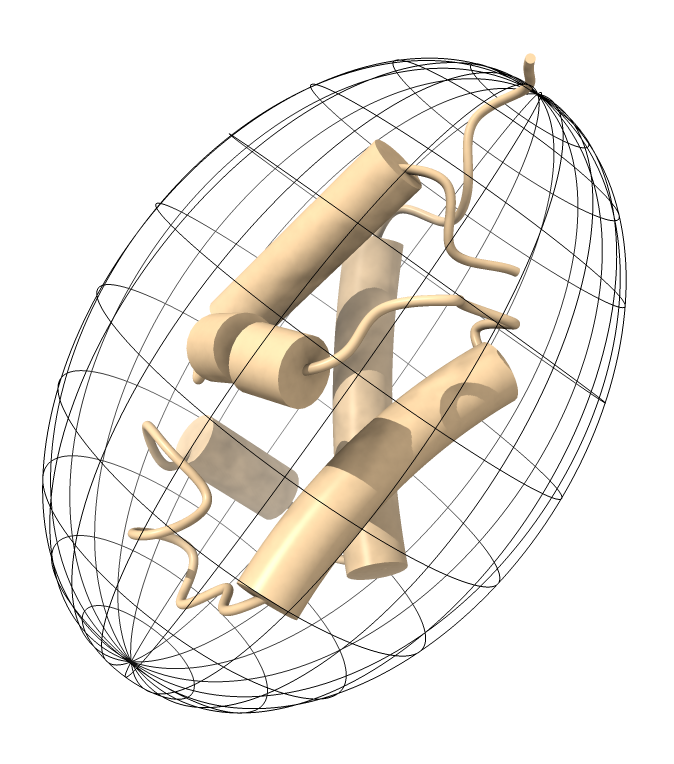
The ChimeraX script has at the top the 4 lines of parameters produced by ROTDIF. Opening the script ELM_ellipsoid_chimerax.py in ChimeraX produces the ellipsoid model.

# Make an ellipsoid depiction in ChimeraX using parameters from
# ROTDIF software http://gandalf.umd.edu/FushmanLab/pdsw.html

# Parameters on the following 4 lines come from end of
# PyMol script produced by ROTDIF.

#1. Center of Mass of the molecule
cmx, cmy, cmz = 20.051, 6.333, -0.915
#2. Ellipsoid semiaxes length (in Angstrom)
a1,a2,a3 = 21.700, 24.645, 16.567
#3. Color: see https://pymolwiki.org/index.php/Color_Values for more options
color = [0.85, 0.85, 1.00]
#4. Rotation Input: three Euler angles: alpha, beta, gamma (in degrees)
rotationInput = [83.790, 114.370, 179.850]



# Make an ellipsoid showing lattitute and longitude lines.
# ChimeraX shape sphere command uses smooth spiral triangulation so cannot be used.
def ellipsoid_mesh(session, name, center, radii, rotation, divisions, color, opacity):
    vertices, edges = lattitude_longtitude_circles(divisions)

    # Stretch, rotate and center
    vertices *= radii
    rotation.transform_points(vertices, in_place = True)
    vertices += center

    # Create ellipsoid model
    from chimerax.core.models import Surface
    s = Surface(name, session)
    normals = None
    s.set_geometry(vertices, normals, edges)
    s.color = [int(255*r) for r in color+[opacity]]
    s.display_style = s.Mesh
    session.models.add([s])

def lattitude_longtitude_circles(n = 10):
    cvertices,cedges = unit_circle()

    vertices = []
    edges = []

    # Make lattitude circles
    from math import pi, sin, cos
    for i in range(n):
        a = pi * (i+1) / (n+1)
        v,e = cvertices.copy(), cedges.copy()
        v *= sin(a)
        v[:,2] += cos(a)
        e += len(vertices)*len(v)
        vertices.append(v)
        edges.append(e)

    # Make longitude circles
    from chimerax.geometry import vector_rotation
    for i in range(n):
        a = pi * i / n
        v,e = cvertices.copy(), cedges.copy()
        normal = (cos(a), sin(a), 0)
        vector_rotation((0,0,1), normal).transform_points(v, in_place = True)
        e += len(vertices)*len(v)
        vertices.append(v)
        edges.append(e)

    from numpy import concatenate
    return concatenate(vertices), concatenate(edges)

def unit_circle(n = 200):
    from numpy import empty, float32, int32, sin, cos, arange, pi
    a = arange(0, 2*pi, 2*pi/n)
    vertices = empty((n,3), float32)
    vertices[:,0] = cos(a)
    vertices[:,1] = sin(a)
    vertices[:,2] = 0
    edges = empty((n,2), int32)
    edges[:,0] = range(n)
    edges[:,1] = (edges[:,0] + 1) % n
    return vertices, edges

def euler_rotation(euler_angles):
    from math import radians, cos, sin
    a, b, g = [radians(a) for a in euler_angles]
    R11, R12, R13 = cos(g) * cos(b) * cos(a) - sin(g) * sin(a), -sin(g) * cos(b) * cos(a) - cos(g) * sin(a), sin(b) * cos(a)
    R21, R22, R23 = cos(g) * cos(b) * sin(a) + sin(g) * cos(a), -sin(g) * cos(b) * sin(a) + cos(g) * cos(a), sin(b) * sin(a)
    R31, R32, R33 = -cos(g) * sin(b), sin(g) * sin(b), cos(b)
    from chimerax.geometry import Place
    rot = Place(axes = ((R11, R21, R31), (R12, R22, R32), (R13, R23, R33)))
    return rot

# Show ellipsoid in ChimeraX
ellipsoid_mesh(session,
               name = 'diffusion ellipsoid',
               center = (cmx,cmy,cmz),
               radii = (a1,a2,a3),
               rotation = euler_rotation(rotationInput),
               divisions = 10,
               color = color,
               opacity = 1.0)

Tom Goddard, March 16, 2021